
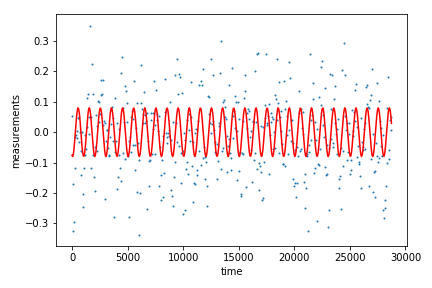
We can use a matrix notation to express the values of this function Our approximating function is the linear combination of parameters to be determined, for example Determined values, of course, should minimize the sum of the squares of the residuals. Here we will demonstrate with linear regression models, then the approximating function is the linear combination of parameters that needs to be determined. You can find more information, including formulas, about the least squares approximation at Function approximation with regression analysis. And the method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems (sets of equations in which there are more equations than unknowns) by minimizing the sum of the squares of the residuals made in the results of every single equation. Linear least squares (LLS) is the least squares approximation of linear functions to data. Note that if the x-values field is left empty, the calculator assumes that x changes starting from zero with a +1 increment. Formulas and a brief theory recap can be found below the calculator, as usual. However, it includes 4th and 5th order polynomial regressions. That's why, unlike the above-mentioned calculator, this one does not include power and exponential regressions.
This poses some limitations to the used regression model, namely, only linear regression models can be used. Lagrange multipliers are used to find a curve-fit in case of constraints. But, unlike the previous calculator, this one can find an approximating function if it is additionally constrained by particular points, which means that the computed curve-fit should pass through these particular points. The calculator below uses the linear least squares method for curve fitting, in other words, to approximate one variable function using regression analysis, just like the calculator Function approximation with regression analysis.


 0 kommentar(er)
0 kommentar(er)
